Escape Time Zooms of the Fibonacci Numbers
 The Fibonacci numbers are usually defined via a recursion: Fn+2= Fn+1 Fn, F0=0, and F1=1. The sequence begins 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,.... These numbers may also be computed via a closed form known as the Binet formula.

It is: 0k where 0k and 0k.
That function can be viewed as a function of a complex variable and we consider here some zooms near two of the fixed points.
34k
fib0.mov
34k
fib5.mov

If the movies do not download, "save target" and run the movie in quicktime.

A J6.02 script which can generate such an image is: fib_v_fig3b.html or an old J5.04 version fib_v_fig3.html Note: I think complex overflow changed between J versions so the images somewhat depending upon version.

See also:
  1. C. A. Reiter, Views of Fibonacci Dynamics, Computers & Graphics 28 2 (2004) 297-300. Preprint [1.7M], [Abstract]
  2. The Fibonacci Association, http://www.mscs.dal.ca/Fibonacci/
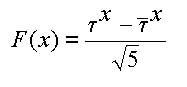
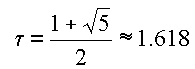
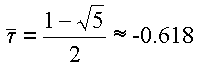
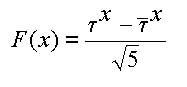
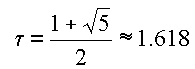
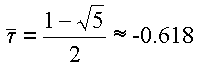