Distance from point	Tiling deformed from square to hexagon	Defective tiling deformed	Distance from point with defects
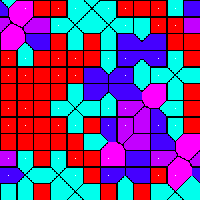
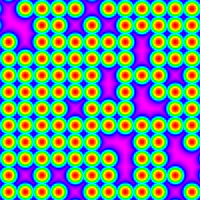
r12000_mag.png	r12000_til.png	rr12000_til.png	rr12000_mag.png
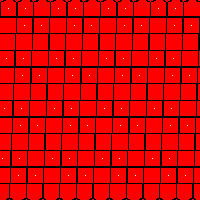
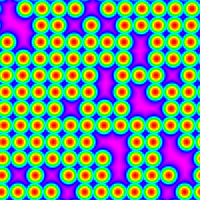
r12001_mag.png	r12001_til.png	rr12001_til.png	rr12001_mag.png
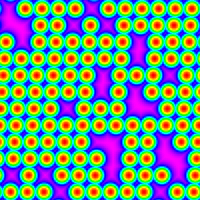
r12002_mag.png	r12002_til.png	rr12002_til.png	rr12002_mag.png
r12003_mag.png	r12003_til.png	rr12003_til.png	rr12003_mag.png
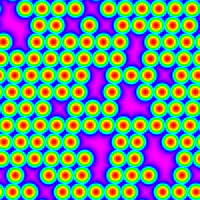
r12004_mag.png	r12004_til.png	rr12004_til.png	rr12004_mag.png
r12005_mag.png	r12005_til.png	rr12005_til.png	rr12005_mag.png
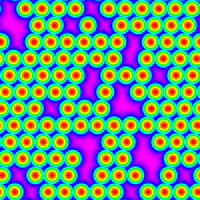
r12006_mag.png	r12006_til.png	rr12006_til.png	rr12006_mag.png
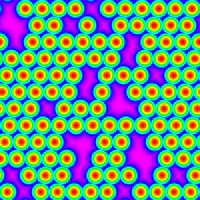
r12007_mag.png	r12007_til.png	rr12007_til.png	rr12007_mag.png
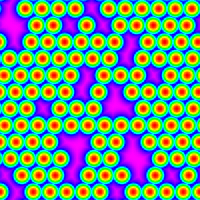
r12008_mag.png	r12008_til.png	rr12008_til.png	rr12008_mag.png
r12009_mag.png	r12009_til.png	rr12009_til.png	rr12009_mag.png
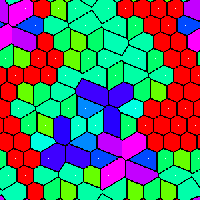
r12010_mag.png	r12010_til.png	rr12010_til.png	rr12010_mag.png
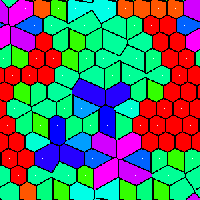
r12011_mag.png	r12011_til.png	rr12011_til.png	rr12011_mag.png
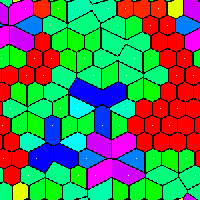
r12012_mag.png	r12012_til.png	rr12012_til.png	rr12012_mag.png

Reference

· Ned W. Allis*, Jeffrey P. Dumont* and Clifford A. Reiter, Visualizing point sets, fractals, and quasicrystals using raster techniques Computers & Graphics, 25 (2001) 519-527 [abstract].