Cauchy curves are created by following the partial path integrals of path integrals known to be zero by Cauchy's Integral Theorem. These galleries augment those described in Cauchy Curves which is on-line in Vector. A script cauchy_curves.html reproduces the figures in that paper.

Some Variantions on Figure 5:
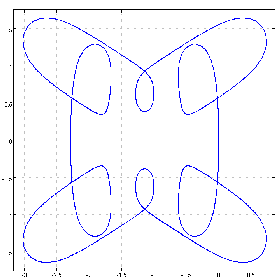
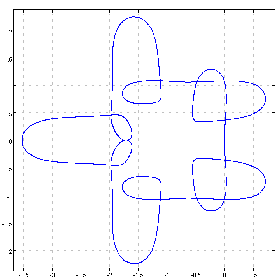
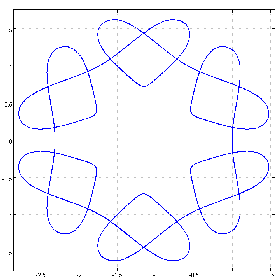
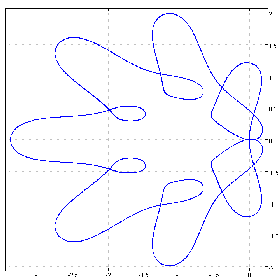
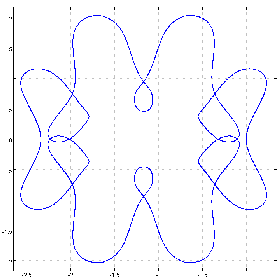
(1 0 0 0 0 0 2&p.%1.01+^&10)chycu lC	(1 0 0 0 0 0 2&p.%1.01+^&11)chycu lC	Figure 5 (1 0 0 0 0 0 2&p.%1.01+^&12)chycu lC	(1 0 0 0 0 0 2&p.%1.01+^&13)chycu lC	(1 0 0 0 0 0 2&p.%1.01+^&14)chycu lC
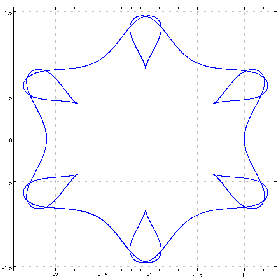
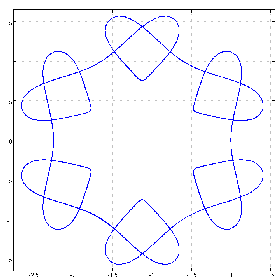
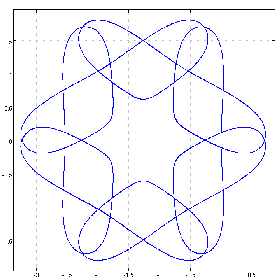
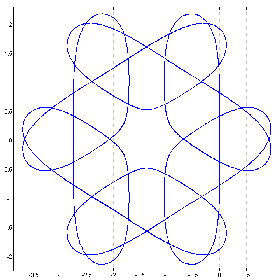
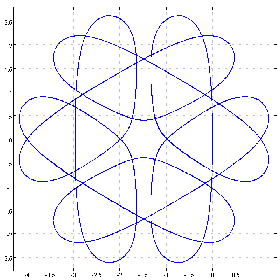
(1 0 0 0 0 0 1&p.%1.01+^&12)chycu lC	(1 0 0 0 0 0 1.7&p.%1.01+^&12)chycu lC	(1 0 0 0 0 0 3&p.%1.01+^&12)chycu lC	(1 0 0 0 0 0 4&p.%1.01+^&12)chycu lC	(1 0 0 0 0 0 5&p.%1.01+^&12)chycu lC
Some other Polynomials:
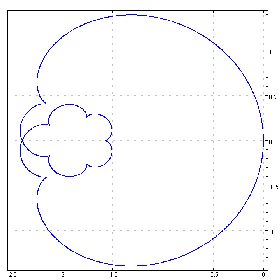
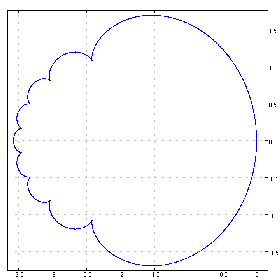
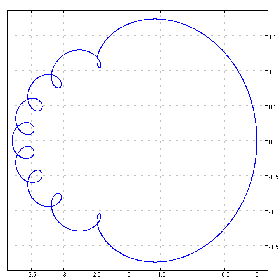
f=. 0 1 1 1 1 1 1 1 1&p. cplot f chycu C	f=. 1 1 1 1 1 1 1 1 1&p. cplot f chycu C	f=. 1 1 1 1 1 1 1 1 2&p. cplot f chycu C
A Family of Polynomials:
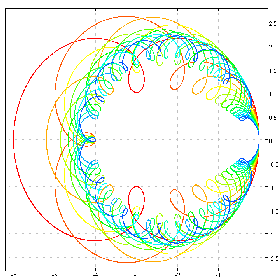
(2+i.12) (2+3*]^[) cfplot C
Some other Families:
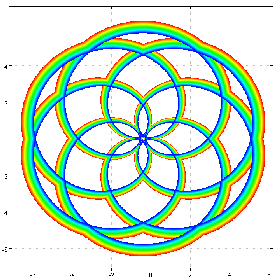
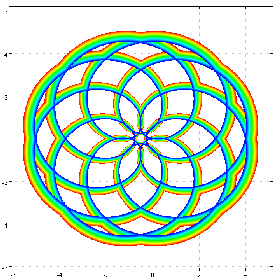
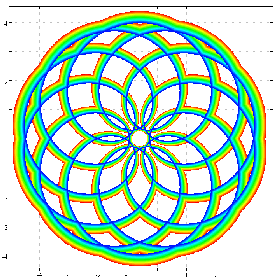
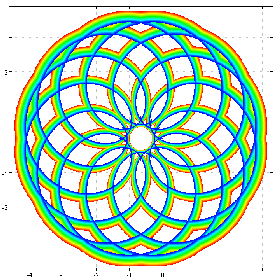
a=:5*0.97^ steps 0 1 50 a cos@:([*^&3@]) cfplot C	a cos@:([*^&4@]) cfplot C	a cos@:([*^&5@]) cfplot C	a cos@:([*^&6@]) cfplot C
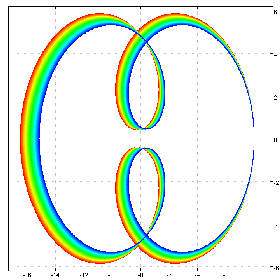
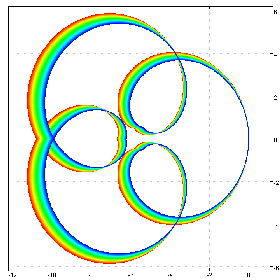
b=:4*0.97^ steps 0 1 50 b ^@:([*^&2@]) cfplot C	b ^@:([*^&3@]) cfplot C
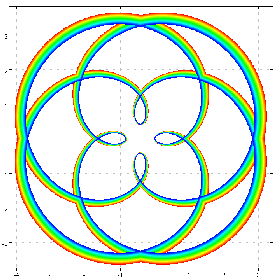
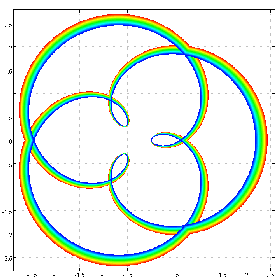
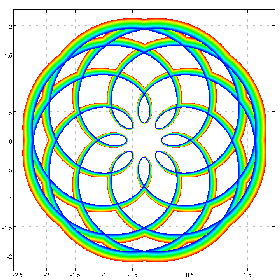
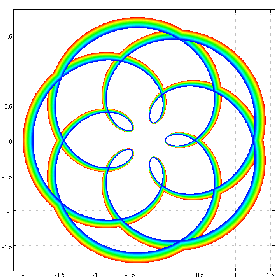
b=:4*0.97^ steps 0 1 50 b sin@:([*^&2@]) cfplot C	b sin@:([*^&3@]) cfplot C	b sin@:([*^&4@]) cfplot C	b sin@:([*^&5@]) cfplot C
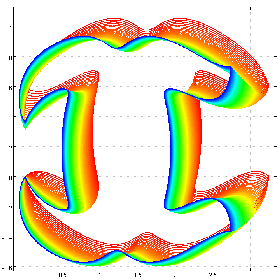
fh6=: 1 0 0 0 0 0 2&p.@] % 1.01+]^[ d=: 12*1.07^ steps 0 0.5 100 d fh6 cfplot ell
Some Alternate Paths:
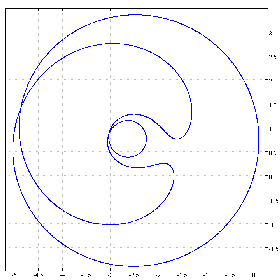
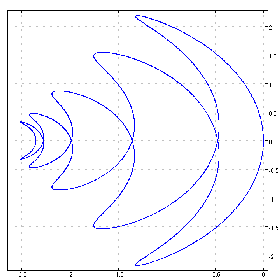
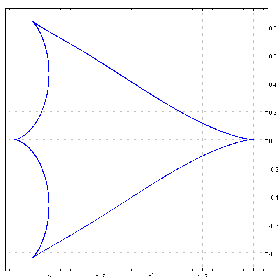
cc=: (cos j. 6*1+sin) steps 0 2p1 10000 cplot ^ chycu cc	cc=. (cos j. sin@(5&*)) steps 0 2p1 10000 cplot ^ chycu cc	cc=. (^&3@cos j. ^&3@sin) steps 0 2p1 10000 cplot ^ chycu cc