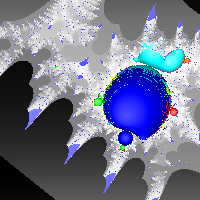
Gallery of images of the escape time of the principal critical point for several q
The complex dynamics of families of functions of the following type are investigated.
F(z)=α (τ z - (τ - ) z ) where τ = ½ (1 + q ½ ) and τ - = ½ (1 - q ½ )
For a fixed q there is a principal critical point, and by following the dynamics of the principal critical point as we vary α, we obtain analoges of the Mandelbrot set. By fixing α, we obtain analoges of filled in Julia sets.

Gallery of images of the escape time of the principal critical point for several q
| Some Extra Wide Views for a few q's (center -5+10i, width 22) | ||
 q=5 |
 q=15 |
 q=610 |
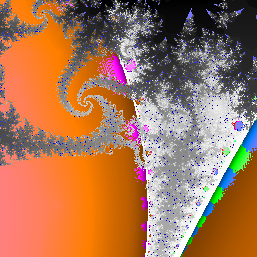
A zoom into q = 5 critical point dynamics. This is a large file (23.5MB).
If your browser does not directly support viewing this *.mov file,
save it locally and view it with Quicktime™.