Canonical projection is used to create 3D quasicrystals. We offer here some verification of "direct computations" along with Mathematica notebooks giving 3D models of figure in the paper. These pages are designed to supplement the manuscript "Computing and Visualizing 3-Dimensional Quasicrystals".

Mathematica notebook that checks the properties in Section 3
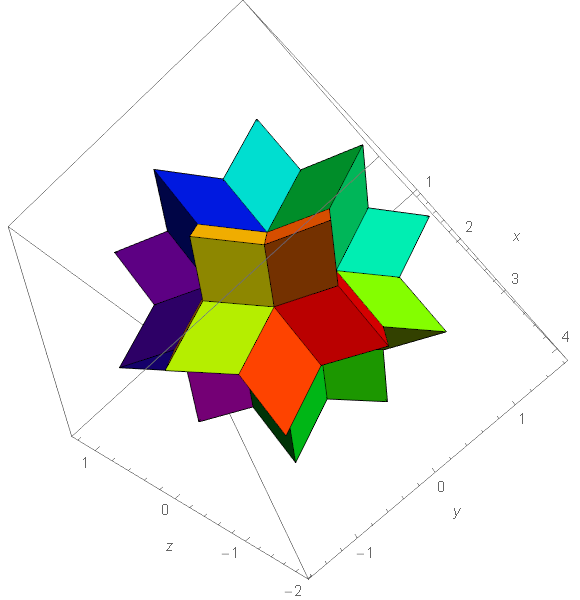
Figure 4. A local configurationn for the I6-quasicrystal
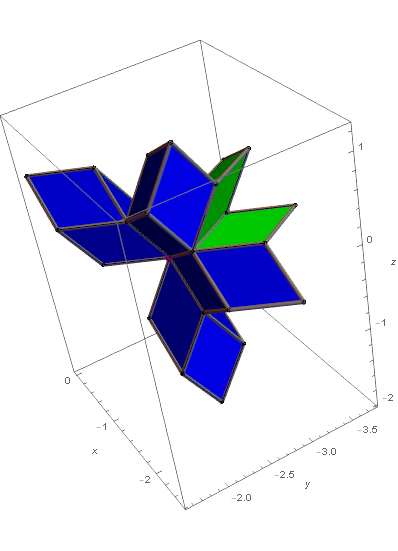Smaller neighborhoods in the I6-quasicrystal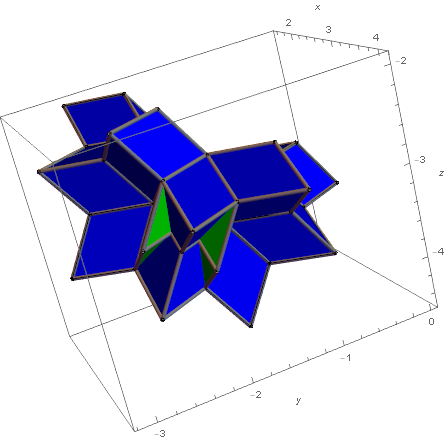
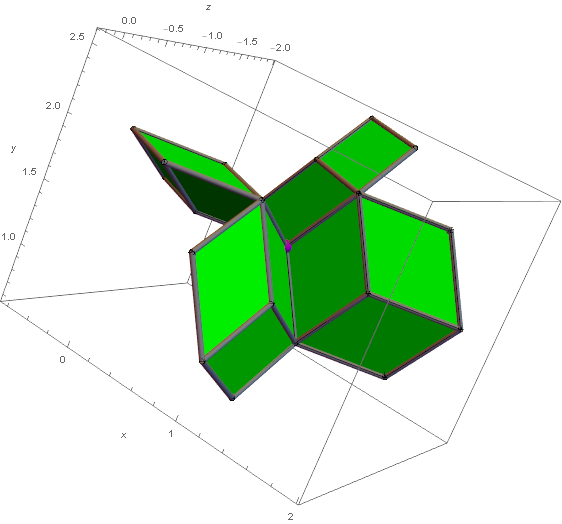
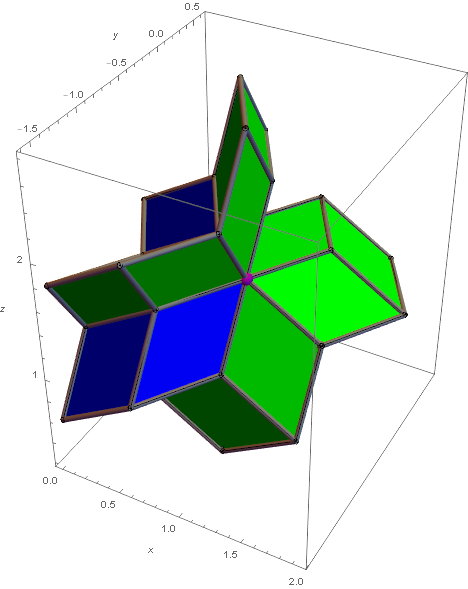
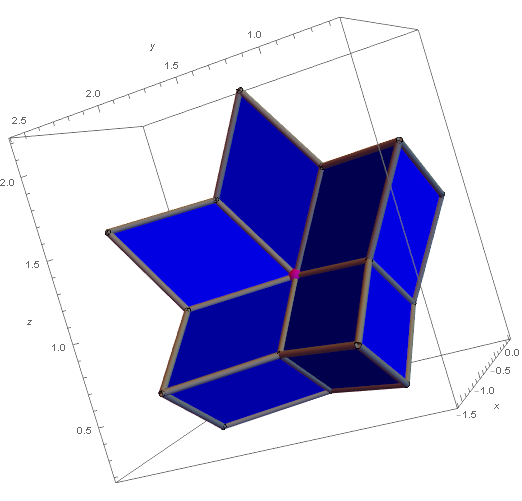
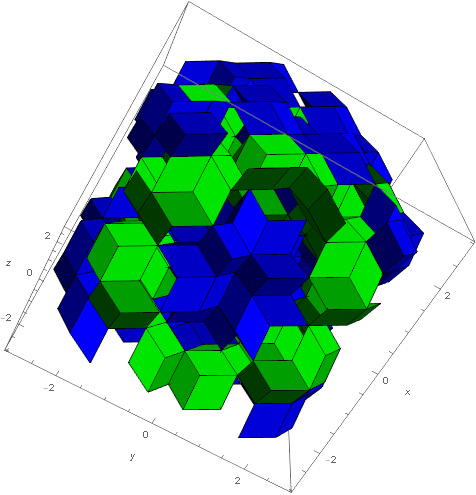
Figure 6. Projecting a bounded range for the I6-quasicrystal
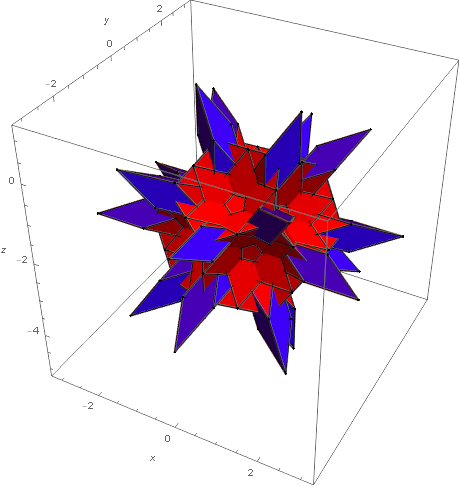
Figure 7. Projecting a bounded range for the I6-quasicrystal
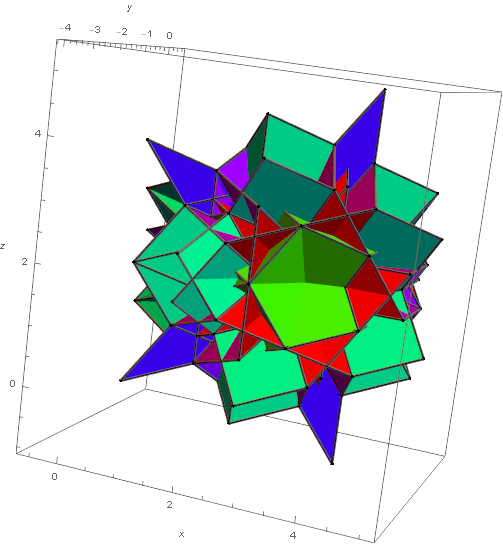
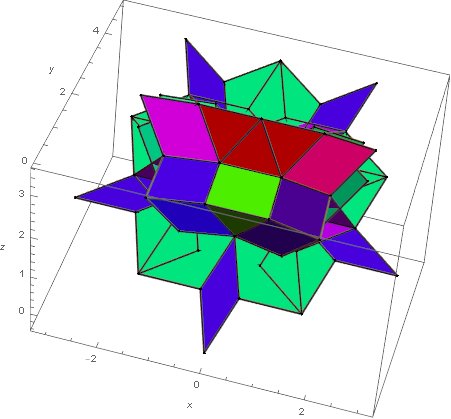
Figure 8. Two neighborhoods for the D6-quasicrystal with 26 and 25 neighbors.
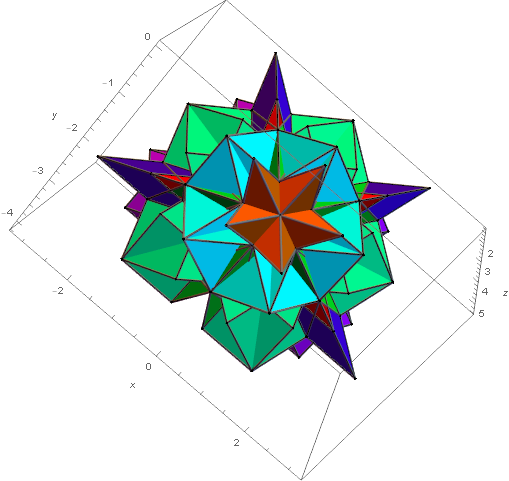
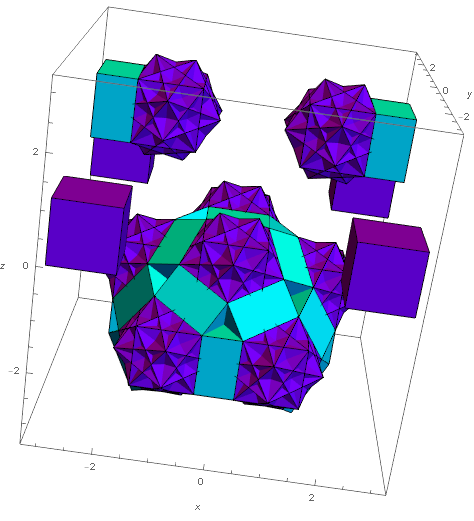
Figure 9. D6-quasicrystal in Q(3)	Two parallelepipeds in Q(6)	All rectangular boxes in Q(3)
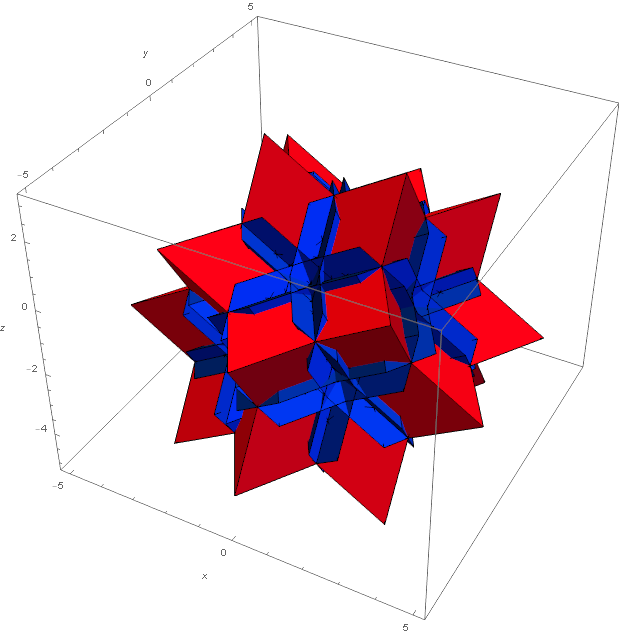
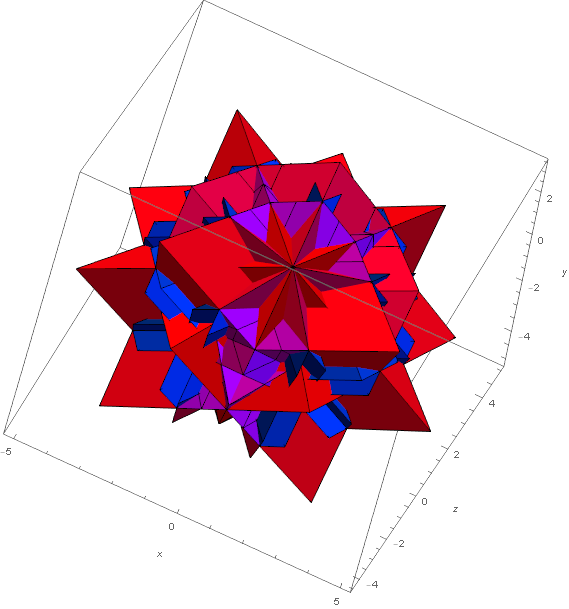
Figure 10a. Neighborhoods in the D6-quasicrystal	Figure 10b
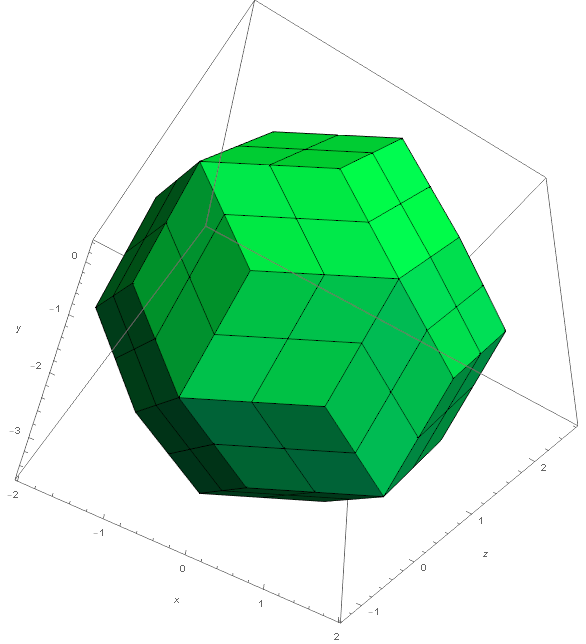
Figure 11a. Restricting Fig 10b to a single parallelepiped	Figure 11b	Figure 11c
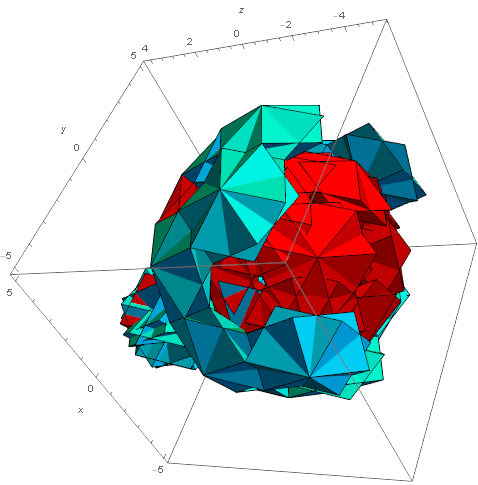
Figure 12. Restricting Q(3) to 2 parallelepipeds in the D6-quasicrystal