![]()
![]()
![]()
![]()
![]()
In[1]:=
![]()
![]()
In[2]:=
![]()
![]()
In[3]:=
![]()
Out[3]=
![]()
In[4]:=
![]()
Out[4]=
![]()
![]()
In[5]:=
![]()
Out[5]=
![]()
In[6]:=
![]()
Out[6]=
![]()
![]()
In[7]:=
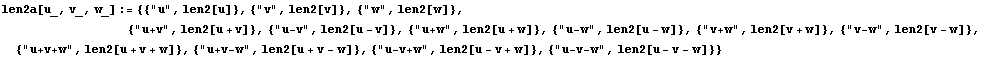
In[8]:=
![]()
Out[8]=
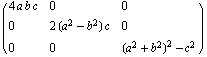
![]()
In[9]:=
![]()
Out[9]=

![]()
In[10]:=
![]()
Out[10]=
![]()
In[11]:=
![]()
Out[11]=
![]()
In[12]:=
![]()
Out[12]=
![]()
![]()
In[13]:=
![]()
Out[13]=
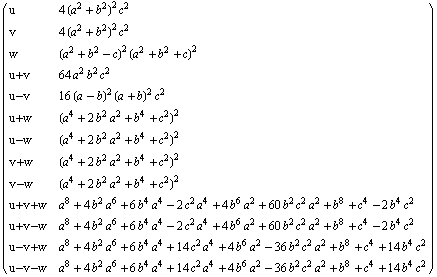
![]()
In[14]:=
![]()
Out[14]=
![]()
In[15]:=
![]()
Out[15]=
![]()
In[16]:=
![]()
Out[16]=
![]()
In[17]:=
![]()
Out[17]=
![]()
In[18]:=
![]()
Out[18]=
![]()
![]()
In[19]:=
![]()
Out[19]=
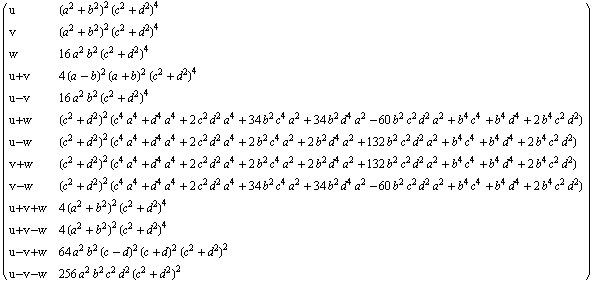
| Created by Mathematica (August 8, 2007) |