Materials for An Infinite Family of Perfect Parallelepipeds
Benjamin D. Sokolowsky, Amy G. VanHooft, Rachel M. Volkert, Clifford A. Reiter
In[1]:=
![]()
Section 2
Section 2.1
Initial Parameterization
In[2]:=
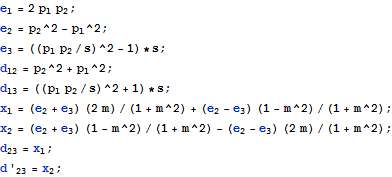
Pythagorian Equation and Parallelogram Law
In[11]:=
![]()
Out[11]=
![]()
In[12]:=
![]()
Out[12]=
![]()
In[13]:=
![]()
Out[13]=
![]()
Body Diagonals
In[14]:=
![]()
In[15]:=
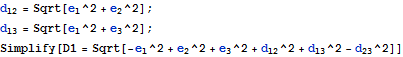
Out[17]=
![]()
In[18]:=
![]()
Out[18]=
![]()
In[19]:=
![]()
Out[19]=
![]()
In[20]:=
![]()
Out[20]=
![]()
Section 2.2
Theorem 2.1
In[21]:=
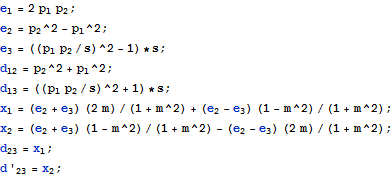
In[30]:=
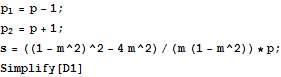
Out[33]=
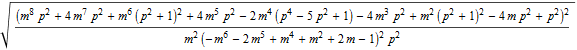
In[34]:=
![]()
Out[34]=
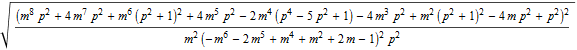
In[35]:=
![]()
Out[35]=
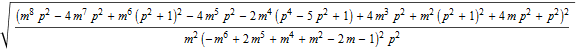
In[36]:=
![]()
Out[36]=
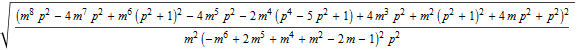
Body diagonals using ![]()
In[37]:=
![]()
Out[37]=
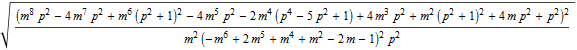
In[38]:=
![]()
Out[38]=
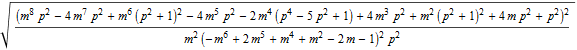
In[39]:=
![]()
Out[39]=
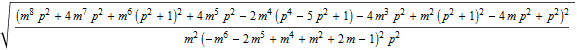
In[40]:=
![]()
Out[40]=
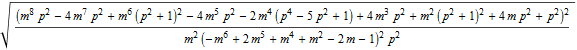
Final Parameterization
In[41]:=
![]()
Out[41]=
![]()
In[42]:=
![]()
Out[42]=
![]()
In[43]:=
![]()
Out[43]=
![]()
In[44]:=
![]()
Out[44]=
![]()
In[45]:=
![]()
Out[45]=
![]()
In[46]:=
![]()
Out[46]=
![]()
Embedding in 3-Space
In[47]:=

In[52]:=
![]()
In[53]:=
![]()
In[54]:=
![]()
Out[54]=
![]()
In[55]:=
![]()
Out[55]=
![]()
In[56]:=
![]()
Out[56]=
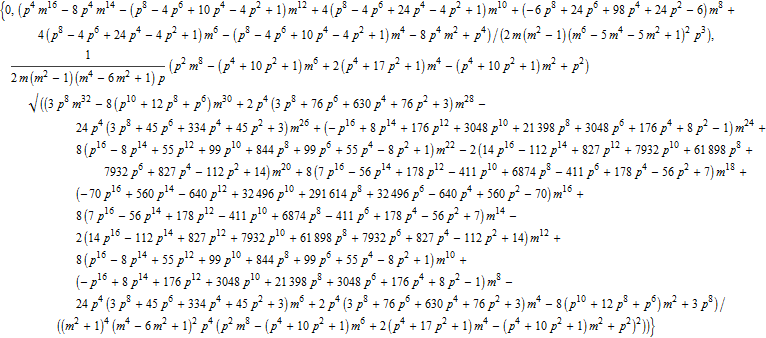
In[57]:=
![]()
Out[57]//MatrixForm=

In[58]:=
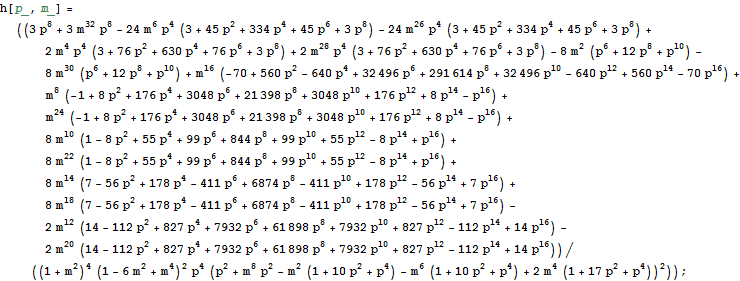
In[59]:=
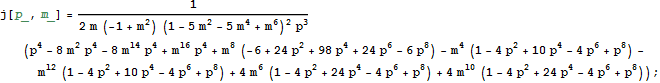
In[60]:=
![]()
Lemma 2.2
In[61]:=
![]()
Out[61]=
![]()
In[62]:=
![]()
Out[62]=
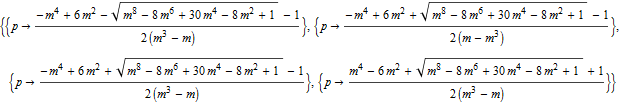
In[63]:=
![]()
Lemma 2.3
In[64]:=
![]()
In[65]:=
![]()
Out[65]=
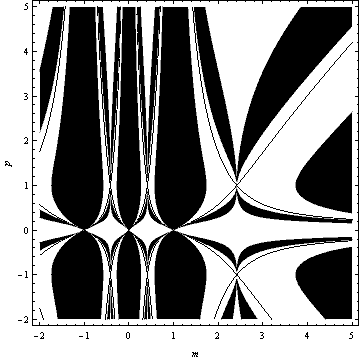
Section 2.3
Theorem 2.6
In[66]:=
![]()
In[68]:=
![]()
Out[68]=
![]()
In[69]:=
![]()
Out[69]=
![]()
In[70]:=
![]()
Out[70]=
![]()
In[71]:=
![]()
Out[71]=
![]()
In[72]:=
![]()
Out[72]=
![]()
In[73]:=
![]()
Out[73]=

Theorem 2.7
In[74]:=
![]()
In[75]:=
![]()
Out[75]=
![]()
In[76]:=
![]()
Out[76]=
![]()
In[77]:=
![]()
Out[77]=
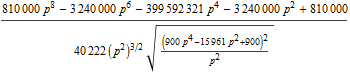
In[78]:=
![]()
Out[78]=
![]()
In[79]:=
![]()
Out[79]=
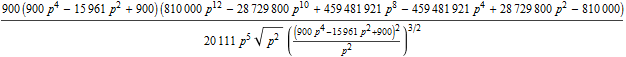
In[80]:=
![]()
Out[80]=
![]()
Section 3
In[81]:=
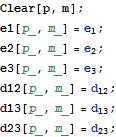
Lemma 3.1
In[88]:=
![]()
Out[88]=
![]()
In[89]:=
![]()
Out[89]=
![]()
Lemma 3.2
In[90]:=
![]()
Out[90]=
![]()
![]()
In[91]:=
![]()
Out[91]=
![]()
Lemma 3.3
In[92]:=
![]()
Out[92]=
![]()
![]()
In[93]:=
![]()
Out[93]=
![]()
![]()
Lemma 3.4
In[94]:=
![]()
Out[94]=
![]()
In[95]:=
![]()
Out[95]=
![]()
Lemma 3.5
In[96]:=
![]()
Out[96]=
![]()
![]()
In[97]:=
![]()
Out[97]=
![]()
![]()
In[98]:=
![]()
In[99]:=
![]()
Out[99]=
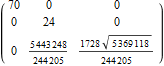
In[100]:=
![]()
Out[100]=

In[101]:=
![]()
Out[101]=
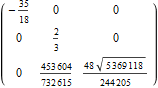
In[102]:=
![]()
Out[102]=

In[103]:=

In[104]:=
![]()
Out[104]=

In[105]:=
![]()
Out[105]=

Section 5
Theorem 5.1
In[106]:=
![]()
Out[106]=

In[107]:=
![]()
In[108]:=
![]()
In[109]:=
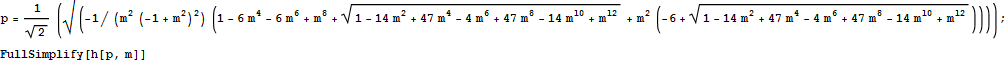
Out[110]=
![]()
In[111]:=
![]()
Out[111]=
![]()
In[112]:=
![]()
Out[112]=
![]()
In[113]:=
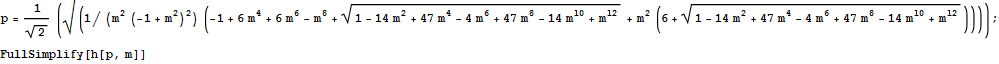
Out[114]=
![]()
In[115]:=
![]()
Out[115]=
![]()
In[116]:=
![]()
Out[116]=
![]()
In[117]:=
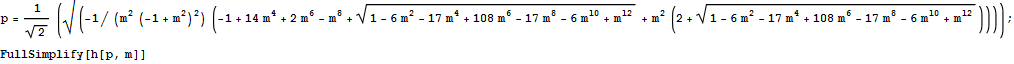
Out[118]=
![]()
In[119]:=
![]()
Out[119]=
![]()
In[120]:=
![]()
Out[120]=
![]()
In[121]:=
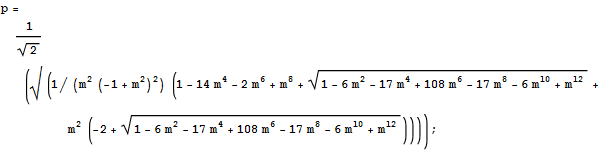
In[122]:=
![]()
Out[122]=
![]()
In[123]:=
![]()
Out[123]=
![]()
In[124]:=
![]()
Out[124]=
![]()
In[125]:=
![]()
In[126]:=

In[127]:=
![]()
In[128]:=
![]()
Out[128]=
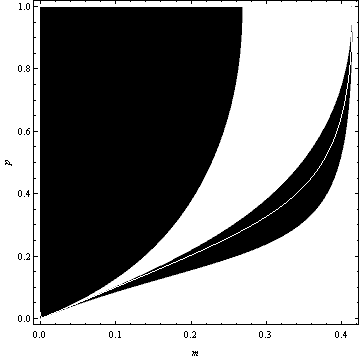
In[129]:=
![]()
Out[129]=
![]()
In[130]:=
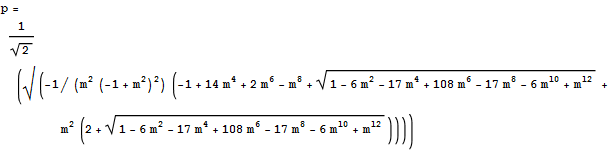
Out[130]=
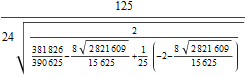
Example after Theorem 5.3
In[131]:=
![]()
In[132]:=
![]()
Out[132]=
![]()
In[133]:=
![]()
In[134]:=
![]()
Out[134]=
![]()
In[135]:=
![]()
Out[135]=
![]()
In[136]:=
![]()
Out[136]=
![]()