Inner Product Fractals from Fuzzy Logics

Auxilary Materials for "Inner Product Fractals from Fuzzy Logics"
by Angela M. Coxe

Paper on the Vector Website: Inner Product Fractals from Fuzzy Logics

Inner products using Boolean "or" and "and" may be used to construct the Sierpinski Triangle from its binary addresses. The first figure below shows such an array as an image and the J expression used to create it. The second figure shows the Sierpinski carpet based upon the generalization of "or" and "and" too "gcd" and "lcm" when a base 3 construction is used.

(+./ . *. |:) #:i.2^8 1=(+./ . *. |:) 3 3 3 3 3#:i.3 ^5

The inner product constructions may also be generalized to using fuzzy logics as the generalization of "or" and "and". In this case, several digit lists with values sampled from [0,1] replace the lists of digits above. The first animation below is based upon the Schweizer family of fuzzy logics; the second is based upon the probabilistic logic where argments are preprocessed by a function that runs through the points (0,0), (0.5,0.5) and (1,1) with a varying slope at 0.5. That is, tw(x)=½+m (x-½)+4(1-m)(x-½)³. We call this the twisted family of logics. The animations were created using a beta version of the J image 3 addon.

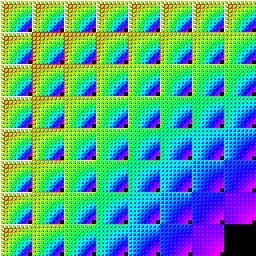Schweizer inner product fractals for a>0

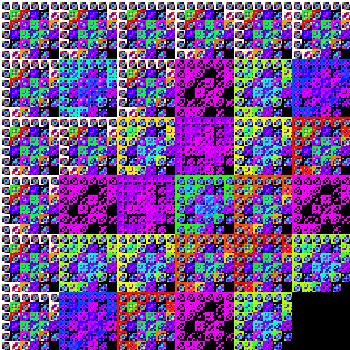Twisted inner product fractals with -3≤m≤1.5.