Auxiliary Materials for Fuzzy Hexagonal Automata and Snowflakes
by Angela M. Coxe and Clifford A. Reiter

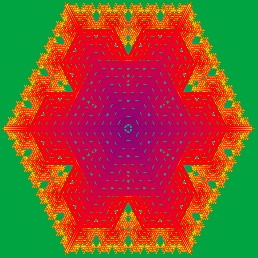
The following illustrations show fuzzy automata on a hexagonal lattice that have been designed to maintain the symmetry of a snowflake. In particular, arithmetic combinations of two level deep neighbors give the new value at any position. The specific combination taken depends upon the configuration of frozen cells in that neighborhood. These models can be made very sensitive to the background level and hence, like snowflakes, readily give rise to a wide diversity of forms. A sample J script for creating images of this type appears below the illustrations.

The first nine animations show the evolution of the automata of a single solid cell in a fuzzy background with the indicated value. The animations range in size from 1-4M.

890k
fz_hx0o1590a.mov
977k
fz_hx0o1700a.mov
1216k
fz_hx0o1730a.mov
1341k
fz_hx0o1762a.mov
1284k
fz_hx0o1778a.mov
1169k
fz_hx0o1788a.mov
1207k
fz_hx0o1800a.mov
1969k
fz_hx0o1880a.mov
4187k
fz_hx0o3000a.mov
The last six animations show variations on the evolution. The first shows the result when two neighboring seed values are frozen. Since the initial configuration does not have the full symmetry of a snowflake, neither do the subsequent images. However, notice the symmetry that does appear. The second example used an initial trianglular configuration with three cells frozen. The last four animations represent the result of a single initial frozen cell in an initial fuzzy background that oscillates between two distinct fuzzy values.
1147k
fz_hx_i2_0o1730_.mov
970k
fz_hx_i3_0o1630_.mov
1743k
fz_hz_os_16_0o1771_0o2000a.mov
1682k
fz_hz_os_16_0o1840_0o2000a.mov
2078k
fz_hz_os_16_0o2000_0o1800a.mov
4241k
fz_hz_os_16_0o2000_0o3000a.mov
Some Links:
· Paper [preprint].
· A J script that creates an image of one of these automata.
· Packard Boolean Snowflake Automata and other Boolean Automata with Snowlake Symmetry.
· Ken Libbrecht's page: Snow Crystals.
· A Local Cellular Model for Snow Crystal Growth.
· A Local Cellular Model for Growth on Quasicrystals.
· Gravner-Griffeath Snowflakes