These images are variants on some of the images that appeared in [1] and readers interested in the full details should consult that reference. The algorithm is explained in many numerical analysis texts and in [2]. In summary, the Rayleigh Quotient algorithm is a method for estimating the eigenvalues and eigenvectors of a matrix M. We view it as beginning with a guess for the eigenvalue, u0 and the eigenvector x0. The eigenvalue estimate is improved by solving the linear system (M-u0 I) x1 = x0 where I is the identity matrix. The eigenvalue estimate is improved by u1=(x1^HM x1)/(x1^Hx1) . The process is iterated until an eigenvalue is found (the system is singular), or a maximum iteration count is reached. In practice, eigenvalues are obtained to high accuracy. The difficulty is in globally determining which eigenvalue is obtained. Our images show the basins of attraction of the eigenvalues. Each image coresponds to x0=1 1 1 or x0=1 1 1 1 according to the size of the matrix and uses various choices for matrix and region of the complex plane for the guess u0.

   
   m2        m3         m6             m8
 1 1 1     1  1 1    1 2 3  4     12 _14  0  4
 9 8 4    9+i 8 4    2 5 6  7      7  _6 _2  4
 5 6 2     5  6 2    3 6 8  9    _10  12 _2 _2
                     4 7 9 10    _18  22 _3 _4

Basins of attraction for m2 with Re(u0) in [ _15, 9]	Basins of attraction for m3 with Re(u0) in [ _15, 9]	Basins of attraction for m6 with Re(u0) in [ _20, 12]
Basins of attraction for m8 with Re(u0) in [ _20, 20]	Basins of attraction for m8 with Re(u0) in [ _80, 80]	Basins of attraction for m8 with Re(u0) in [ _320, 320]

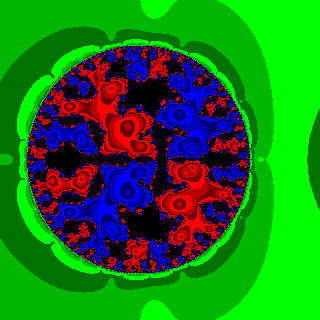Basins of attraction for m2 with Re(u0) in [ _15, 9]

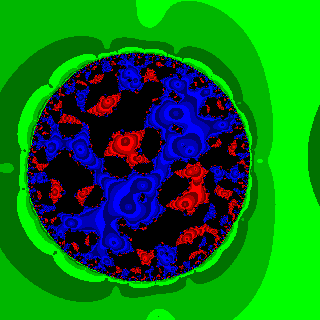Basins of attraction for m3 with Re(u0) in [ _15, 9]