Auxiliary Materials for Sierpinski Word Fractals
by Gabe Brisson and Cliff Reiter
The Sierpinski triangle may be viewed as the attractor of an iterated function system which consists of a contraction by half, along with contractions by half followed by a translation by half along each of the two axes. This is readily generalized to higher dimensions by including all the axes in the dimension. These higher dimensional fractals may be visualized by rendering each axis in a direction equally spaced around a cone [1]. This scheme allows much of the symmetry of higher dimensional fractals to be observed and connections with the chaos game become apparent.
981k
2-D (sws02.mov)
2390k
3-D (sws03j.mov)
2666k
4-D (sws04j.mov)
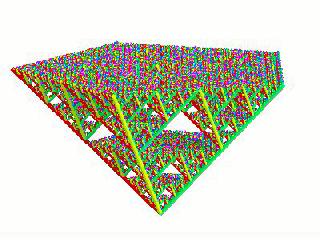
2818k
5-D (sws05j.mov)
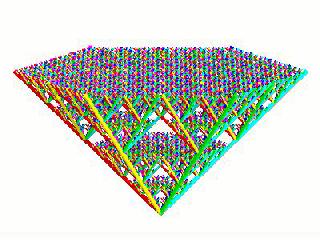
2963k
6-D (sws06j.mov)
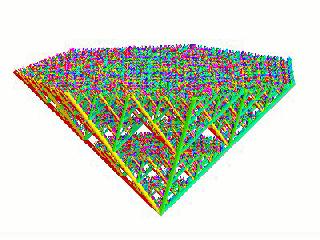
2892k
7-D (sws07j.mov)
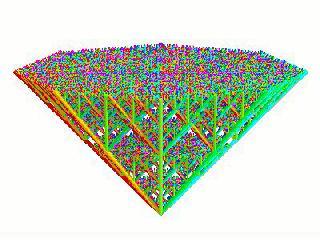
2893k
8-D (sws08j.mov)
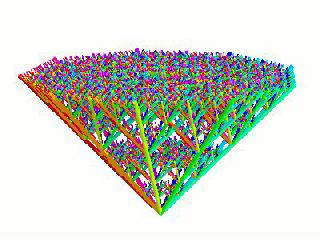
2816k
9-D (sws09j.mov)
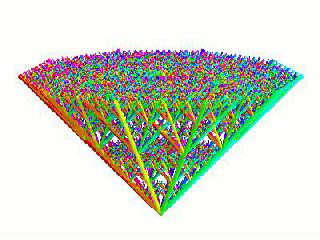
2780k
10-D (sws10j.mov)
See Also:
Work described here is essentially from:
· [1] Gabriel F. Brisson and Clifford A. Reiter, Sierpinski Fractals from Words in High Dimension, Chaos, Solitons & Fractals, 5 11 (1995) 2191-2200. [Abstract mv_1995b]
· A sample J script.
· Some images somewhat related to the paper [Images]
· A paper focusing on Sierpinski Fractals from inner products [Abstract mv_1993]
· A paper focusing on Sierpinski Fractals from GCDs [Abstract mv_1994c]
· A paper on various ways to implement the Sierpinski Triangle in J [Abstract ci_1997a]