Inner Product Fractals

Images of Some Generalized Inner Product Fractals

Here we display some "fractal" images based upon the ordinary matrix product of a matrix of k-digit base-b indices with its transpose. Using J notation , the ordinary matrix product is denoted by +/ . * which can be read as "sums of pairwise products" and the transpose of M is denoted by |: M resulting in arrays shown below. Hence a matrix M times its transpose is M +/ . * |: M .

  M          M +/ . * |: M
0 0 0       0 0 0 0 0 0 0 0
0 0 1       0 1 0 1 0 1 0 1
0 1 0       0 0 1 1 0 0 1 1
0 1 1       0 1 1 2 0 1 1 2
1 0 0       0 0 0 0 1 1 1 1
1 0 1       0 1 0 1 1 2 1 2
1 1 0       0 0 1 1 1 1 2 2
1 1 1       0 1 1 2 1 2 2 3

The images in the table show the result of such computations when various bases are used. Some similar images appear in [1,2].

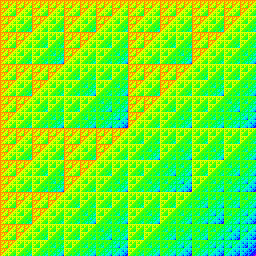
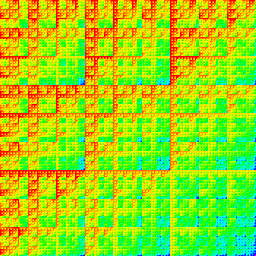
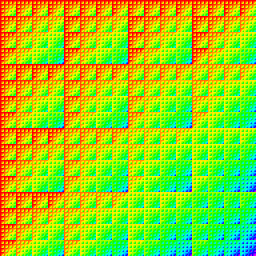
Matrix product of 9-digit base-2 indices.	Matrix product of 6-digit base-3 indices.	Matrix product of 4-digit base-4 indices.
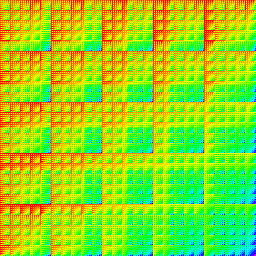
Matrix product of 4-digit base-5 indices.	Matrix product of 3-digit base-6 indices.	Matrix product of 3-digit base-7 indices.

In [2,3] various methods of constructing Sierpnski triangle fractals were explored. Several of those involved a product, base 2, of a matrix of indices with a generalized matrix product. The "matrix product" is generalized in the sense that the "sum" and "pairwise product" operations in ordinary matirx arithmetic are replaced by other functions. Thus, each position in the matrix is the result of applying some operation (like sum) to the pair operation (like product) of the binary vectors represeting the row and column indices.

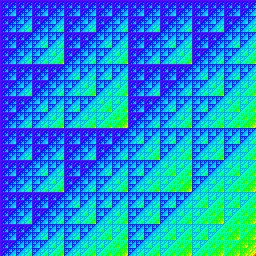
Sums of pairwise nands.

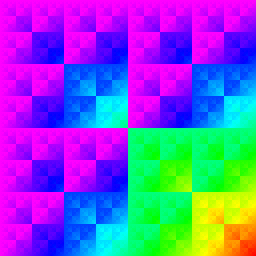
Reinterpret the pairwise nand as an integer.

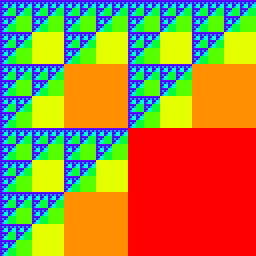
Find the position of the first 0 in the pairwise nand.

The generalized matrix product, using gcd and lcm in place of addition and multiplication gives especially interesting results [4].

Gcd-lcm product of 9-digit base-2 indices.	Gcd-lcm product of 6-digit base-3 indices.	Gcd-lcm product of 4-digit base-4 indices.
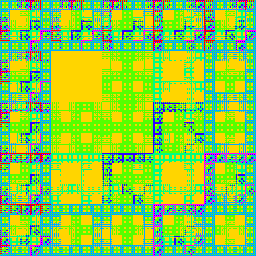
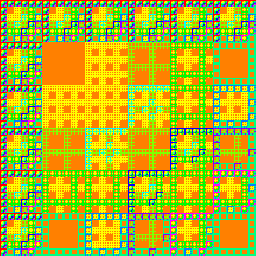
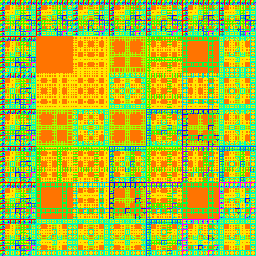
Gcd-lcm product of 4-digit base-5 indices.	Gcd-lcm product of 3-digit base-6 indices.	Gcd-lcm product of 3-digit base-7 indices.

Scripts

A short J script ipf_ex.ijs to create several images of this type.
It requires raster5.ijs as well (installed in the fvj2 subdirectory of the J directory).

References

Clifford A. Reiter, Fractals, Visualization and J, 2nd Edition, Jsoftware, Inc., Toronto (2000)
Clifford A. Reiter, Fractals and Generalized Inner Products, Chaos, Solitons & Fractals, 3 6 (1993) 695-713.
Cliff Reiter, With J: 101 Ways to Build a Sierpinski Triangle, APL Quote Quad, 27 4 (1997) 8-16.
Clifford A. Reiter, Sierpinski Fractals and GCDs, Computers & Graphics, 18 6 (1994) 885-891.

Goto link:
Cliff's Front Page
Cliff's Gallery of Fractals, Chaos and Symmetry