 c1 * c2 |
 c1 * c3 |
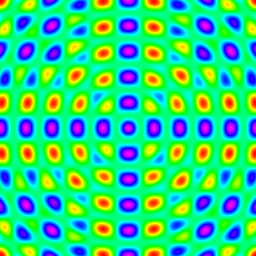 c1 * c2 * c3 |
 s1 * s2 |
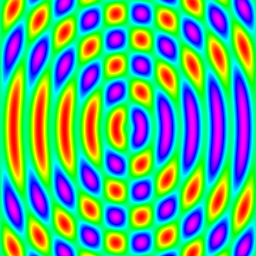 s1 * s3 |
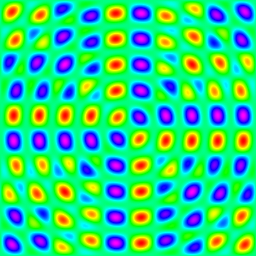 s1 * s2 * s3 |
 c1 + c2 |
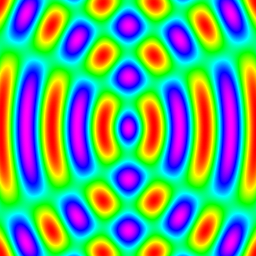 c1 + c3 |
 c1 + c2 + c3 |
 s1 + s2 |
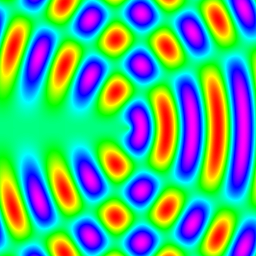 s1 + s3 |
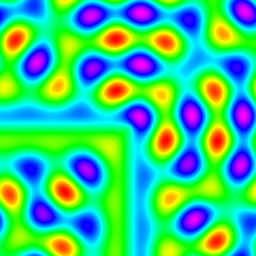 s1 + s2 + s3 |
c1=cos(x), c2=cos(y), c3=cos(r) s1=sin(x), s2=sin(y), s3=sin(r) where r^2=x^2+y^2
 c1 * c2 |
 c1 * c3 |
 c1 * c2 * c3 |
 s1 * s2 |
 s1 * s3 |
 s1 * s2 * s3 |
 c1 + c2 |
 c1 + c3 |
 c1 + c2 + c3 |
 s1 + s2 |
 s1 + s3 |
 s1 + s2 + s3 |
 Animation changing from c1 + c2 to c1 + c2 + c3 to c1 + c3 (1.4M) |
 Animation changing from s1 + s2 to s1 + s2 + s3 to s1 + s3 (1.3M) |